Sigma 30 mm f/1.4 EX DC HSM
4. Image resolution
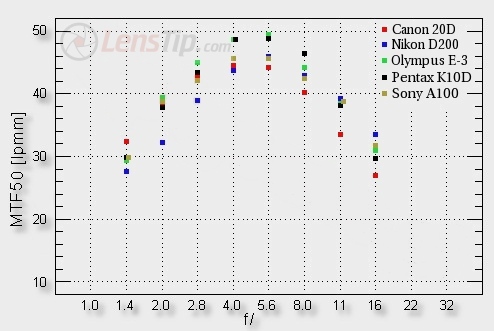
As a matter of fact we can see a few effects here. Firstly, the curve rises with stopping down, which means that the resolution of the obtained images increases. It’s an effect of lowering optical aberrations of the lens, which lessen together with cutting off light from the most outer areas of the lenses system. At around f/4.0-5.6 the lens reaches its peak performance. There, optical aberrations are very small and diffraction comes to the fore. It is also the cause of lowering image quality with stopping down, for apertures larger than f/5.6.
Please Support UsIf you enjoy our reviews and articles, and you want us to continue our work please, support our website by donating through PayPal. The funds are going to be used for paying our editorial team, renting servers, and equipping our testing studio; only that way we will be able to continue providing you interesting content for free. |
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
You need to look differently at a graph where the main limit are optical aberrations, and differently at an area where the limit is diffraction. In this second area all lenses acquit themselves equally, as optical aberrations have no further influence on image quality and optical construction, and used anti-reflection coatings are the same. The differences of the plots of MTF50 function are, then, caused by a used sensor. It’s no wonder, then, that the lowest results are obtained on Canon 20D which has the lowest linear density of pixels, and the biggest for Olympus E-3 which has this density the highest. In-between values are recorded by DSLRs with medium linear densities, so Sony A100 and Nikon D200.
There may be a problem with Pentax K10D, which of all cameras is the worst for testing lenses – this not being an accusation, but stating the fact. One of its coordinates is sharpened even in RAW files (measured results reach non-physical values of 2000 LWPH, so 63 lpmm) and it’s not included in the graph. In the case of testes conducted on Pentax we only use one black-white borderline (vertical), then, thus making less measurements on Pentax, with higher errors.
To better illustrate the problem, let’s have a look at vertical and horizontal MTF curves for Canon 20D and Sigma set at f/4.0, which we’ve shown below.
 |
As you can see there are no major differences between the two curves, so nothing arouses our concerns.
Let’s see how the situation looks at the same aperture with Pentax K10D.
 |
While the graph of the vertical borderline looks naturally, for the horizontal borderline we can’t draw such a conclusion. Unnaturally high MTF50 values, reaching almost 1900 LWPH (for other apertures and lenses tested on K10D we sometimes find values exceeding even 2000 LWPH), reaching 35% answer in Nyquist frequency – all these things suggest that we’re dealing with some serious manipulation in the picture and makes us discard in our analysis values of horizontal borderlines.
Additionally, systematically higher results obtained on vertical borderlines with Pentax K10D than with Sony A100 and Nikon D200, although using sensors of the same producers, with the same amount of pixels, may suggest that apart from one strongly sharpened coordinate, the other one is sharpened slightly as well.
For the maximum aperture range, often higher importance than the number of pixels, has the quality of used optics. You can see that in Sigmas tested on Canon and Nikon. The first one reaches higher results despite a worse sensor. That’s the effect of higher astigmatism of Sigma on Nikon’s mount, something we’ll write about in the proper chapter.
Another problem is the behavior of the lens maximally stopped down. Here, f/16 gives us an actual opening of less than 2 mm. When we add the information of an eight-bladed diaphragm, it turns out that due to imprecision of the overlapping blades, f/16 is sometimes f/15 in one copy and f/17 in another. From the graph we can see a few important for us things as well. Firstly, the behavior at the maximum aperture is acceptable, as in all systems it stays around 30 lpmm, and so the borderline of decency. With stopping down the situation improves quickly, to record results worthy of very good fixed focal lengths at f/4.0-5.6, which confirms that Sigma 1.4/30 mm is very good for testing the quality of sensors used in DSLRs.
Another thing is the divergence of the results illustrated on the graph above, when compared to those at PhotoZone. Our foreign competition shows a much better behavior of Sigma in the maximum aperture range. We think we know the reason for this divergence. This is the effect of testing resolution only on one (probable vertical) black-white borderline. This system of tests isn’t capable of taking into account the influence of a lens’ astigmatism, it being large in Sigma, something we’ll describe more thoroughly in the further chapters. Our tests based on both vertical and horizontal borderlines not only give more test values to average, but also allow to measure the influence of astigmatism.
Let’s go now to Sigma’s behavior at the edge of the frame, which is illustrated on the graph below.
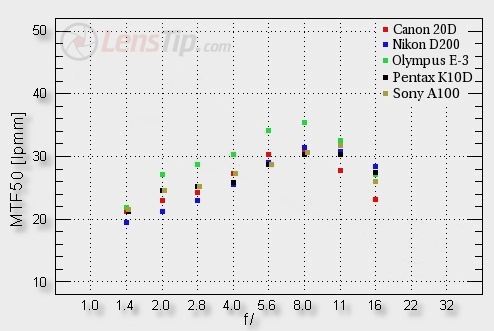
As you can see, contrary to the center of the frame, we have a lot of reasons to complain here. The maximum aperture range is basically useless, and if we want to obtain good image quality at the edge of the frame, we need to stop down the lens to at least f/5.6. It’s not a result we’d expect of a lens of these parameters. To speak positively of Sigma, useful pictures should be obtained at apertures in the range of f/2.0-2.8. In the current situation our assessment of the behavior at the edge of the frame is low.
At the end it’s worth to notice one more thing. The highest values obtained for Olympus at the edge of the frame is not only the effect of its smallest pixels, but also the format of the sensor. In the 4/3 system the edge of the frame is closer to the center than in case of APS-C, and so the lens can perform better. It’s worth to remember, though, that this is at the cost of the angle of view, which in the case of the 4/3 system is the smallest.






